泵轴临界转速的基本概念

轴临界转速的基本概念

泵轴除校核强度外，要进行刚度计算。刚度计算包括两部分内容:第一是计算轴的挠度，使轴在运转中的挠度小于转子和壳体间的平径间隙。轴运转中的挠度等于转子自重引起的静挠度，加土残余不平衡质量的离心惯性力引起的动挠度。但是精确地确定转子的残余不平衡质觉及位置是很困难的，所以一般只用转子自敢引起的静挠度，作为近似的比较标准。第二是一计算轴的临界转速.以保证转子的平稳运转。

共振和临界转速

观察旋转中的轴，可以发现，当轴的转速由启动增加到某一转速时，轴运转变为不稳定，产生较强烈的反复变形和振动。可是，如果继续升高轴转速，会连续反复出现上述现象，我们称这种现象为共振现象，产生共振的转速称为轴的临界转速。引起第一次共振的转速称为第一临界转速，引起第二次共振的转速称为第二临界转速，以此类推。

我们主要研究第一临界转速。

下面，对上述现象作简单的理论分析，以便了解临界转速的实质和决定临界转速的主要因素。

图21--23表示的是质量为m的圆盘，装在两支点的垂直轴中间，以角速度。旋转时的状态。为研究方便，不计轴本身的质量，图中O表示轴心一轴承连线和圆盘的交点，O1表示几何中心一圆盘儿何对称中心与轴心的交点.O2表示圆盘的重心。由于材料的质量不均匀和不可能做到理想平衡等原因，圆盘重心O2与几何中心O1不重合，其偏心距用。表示。

因为轴垂直放置，所以当轴静止时，轴心线与轴承连线重合，轴不产生扰度;当轴开始旋转时，因为有偏心e，则圆盘重心O2，以偏心距e为平径绕轴承连线作圆周运动。由此产生的离心惯性力使轴变形，引起动扰度yd。所以轴旋转起来之后其圆盘重心O2，是以半径r- e+ yd绕轴承连线作圆周运动。这时作用在圆盘上的离心惯性力为

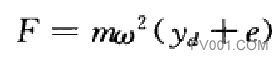
式中m-一圆盘的质量，kg;

w--一轴旋转的角速度，rad/s;

yd一动绕度，m

轴变形后，在轴内产生抵抗变形的内力，此力为轴的弹性力，用P表示。在弹性限度内，轴的弹性力与扰度yd(变形)成正比，即P =Kyd

K称为轴的刚性系数，是轴产生单位变形的弹性力(N/m）。其值表示轴的刚度大小。K值与轴的材料、尺寸、支撑特点和载荷分布等因数有关。

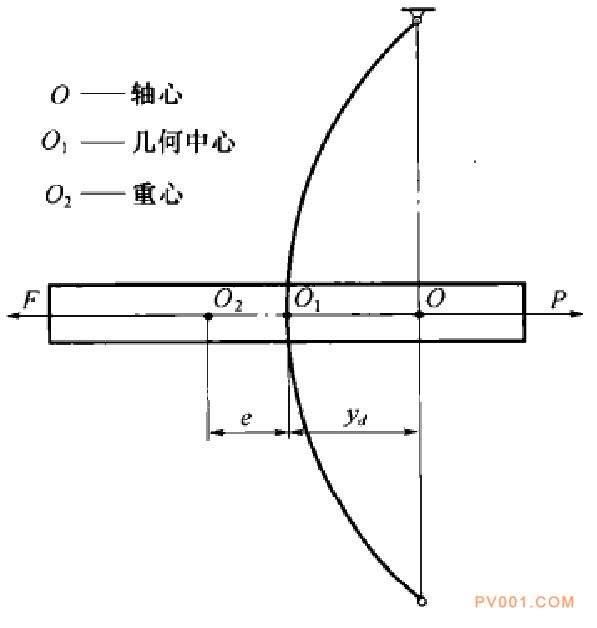
图21一23 垂直轴装单圆盘转子的转动情况

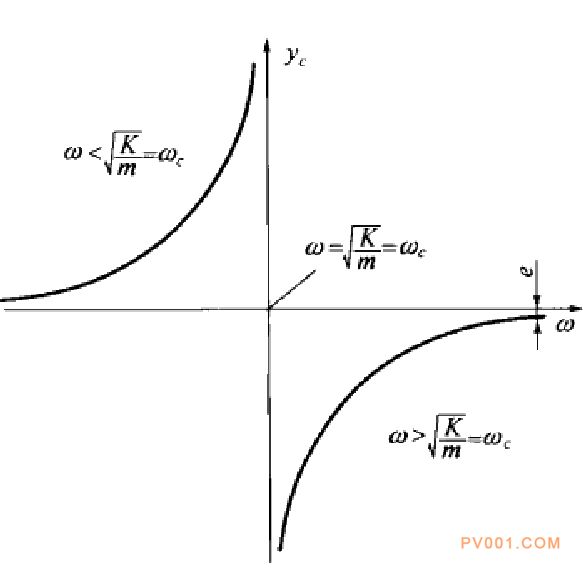
图21一24 轴扰度y与角速度w的关系

离心惯性力F的作用是力图增加轴的扰度，使轴产生变形，增加偏心e而弹性力p是力图减小轴的扰度，恢复原来的形状。在平衡状态下，离心惯性力与所有扰度下的轴的弹性力相平衡。即两力大小相等，方向相反。由平衡条件可以写成

对于给定的轴e、K、m为定值，故扰度yd随角速度。而变化。取yd为纵坐标，w为横坐标，按公式画出两者的关系曲线，如图21一24所示。

式(21---25)表面上看是yd和w的关系式。实际上它是反映了离心惯性力和弹性力的平衡口显然w。代表平衡的一方—离心惯性力;为代表平衡的另一方—轴的弹性力。

随着w的增加，在不同的发展阶段，离心惯性力和轴的弹性力有不同的表现形式，而反映出轴有不同的变形(扰度)的特性.

(1)当w=0时，因轴不旋转，所以为yd=0，圆盘中心O1在轴承连线上，与轴心O相重合，与重心佼的距离为e几何重心O1重心O2与轴心O的关系如图21-25〔a)所示。

(2)当w从O逐渐增加，在上式的分母没有变成负值之前，yd为正值，且随着。的增加而增大。在此阶段内，轴在所有扰度下，弹性力和离心惯性力相平衡。几何中心O1重心O2与轴心O的关系如图21一25 (b)所示。

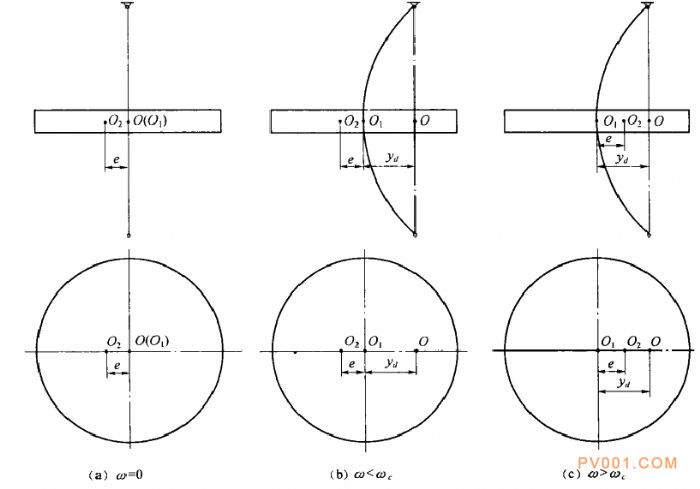
图21一25 不同转速下圆盘几何中心O1重心O2与轴心O的位置关系