钻井液离心机转鼓内流场的数值分析

钻井液离心机转鼓内流场的数值分析

    徐　倩1　孟繁如2　刘洪斌1　张明洪1

          (1·西南石油大学机电工程学院　2·中国石油大庆石化公司)

    摘要：目前,对离心机内流场的计算一般都是从离心机流场的稳态方程出发,着重关注流场在稳定状态下的流动状况,情况复杂时,直接通过稳态方程求解不能准确反映离心机内流场的流动状况。尝试运用Fluent软件对钻井液离心机转鼓内部流场进行模拟分析计算,应用RNGκ-ε模型预测离心机的流场,建立了离心机流道的湍流模型和多相流模型。离心机内流场的分析主要包括速度场、压力场、各相体积分数分布及流道内处理液的轨迹,模拟分析结果与实际情况相符。所得结果将有助于离心机的流场研究。

    关键词：离心机　固控系统　离心机内流场　数值分析

    0　引　言

    钻井液中固相的含量及颗粒大小对钻井液的性能有很大的影响。通常在钻井过程中通过固控设备来控制钻井液中固相的含量,即固相控制。现代钻机的成套固相控制设备一般由钻井液振动筛、除气器、除砂器和离心机等组成,用于逐级清除不同粒度的固相颗粒[1]。其中,钻井液离心机是固控设备中结构最复杂、井队最难掌握的设备。

    目前,国产钻井液离心机都属于卧式螺旋卸料沉降离心机,其转鼓内部流场理论主要有:活塞式流动状态、层流流动状态、表面层流动状态和流线流动状态[2]。然而,这些理论都未能真实反映离心机转鼓内的流场状态。已有文献关于离心机内流场的计算一般都是从离心机流场的稳态方程出发,着重关注流场在稳定状态下的流动状况。情况复杂时,直接通过稳态方程求解不能准确反映离心机内流场的流动状况[3]。笔者将尝试运用Fluent软件对钻井液离心机转鼓内部流场进行分析计算。

    1　离心力场中钻井液流动速度分析[4]

    1·1　基于Σ理论的钻井液流速

    按照Σ理论,钻井液流动时沿轴线方向的速度Vz*与该处液体断面的面积成反比,即：

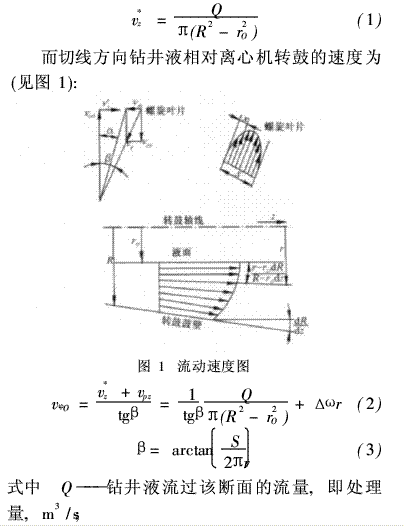
    R———溢流断面的外径, m;

    rO———溢流断面的内径, m;

    r———卸料螺旋在溢流断面的半径, m;

    Δω———钻井液离心机转鼓和卸料螺旋的转速差, s-1;

    vpz———卸料螺旋叶片运动引起钻井液在轴线方向的分速度, m/s;

    β———卸料螺旋升角, (°);

    S———螺距, m。

    1·2　紊流状态下离心力场中钻井液流动速度

    实际上,钻井液在沿卸料螺旋的流动过程中,由于具有较大的流动速度,流体处在紊流状态下流动。根据粘性流体力学理论,在紊流状态下采用统计平均方法,用时均速度来代替流体在某点的流动速度。

    流体在沿槽流动时,该断面上某处流体的流动速度v与平均速度具有以下关系：

    2　三维模型的建立

    2·1　湍流模型

    在所有的双方程模型中,κ-ε双方程模型的应用最为普遍。但是由于它采用了同向性湍流输运的假设,故不适应具有非同向性湍流输运的强旋流。在离心分离器内流场中,因切速度远远大于径向和轴向分量,因而采用雷诺应力模型(RSM)、代数应力模型(ASM)或RNG模型来代替κ-ε模型。RNG模型对强旋流流场及高曲率流线的离心分离器有着很好的改进效果[5]。笔者应用RNGκ-ε模型预测离心机的流场。

    2·2　多相流模型

    离心机主要是分离在连续液相中分散的固体颗粒,可选用混合模型或欧拉模型。以下为混合模型和欧拉模型的求解策略。

    启动混合模型求解,采用0·2或更小的滑流速度欠松弛因子开始计算。如果解显示出好的收敛趋势,可逐渐增加欠松弛因子。初始计算可以不求解题解分数和滑流速度方程,当计算收敛后,再求解这些方程。

    启动欧拉模型求解,为了提高收敛性,在求解多相流模型前可以先获得初始解再继续计算。初始解可通过混合模型得到。在下面的计算中采用欧拉模型求解。

    2·3　计算前处理

    计算前处理主要包括卧式螺旋离心机三维流道模型的建立及网格划分。采用Pro/E建模, Fluent的前处理器Gambit来实现网格的划分。

    2·4　三维模型的建立

    以LW450-1000型离心机处理非加重钻井液为例,对离心机内流场进行数值分析。离心机和钻井液的参数如下:转鼓半锥角α=8°;转鼓的转速n=1 600 r/min;转鼓内半径R1=225 mm;转鼓内筒外半径R2=152mm;柱筒段沉降区长度L1=582mm;螺距S=108 mm;螺旋升角β=7·59°;处理量为0~60 m3/h;水基非加重钻井液固相密度ρ2=2 030 kg/m3,液相密度ρ1=1 000 kg/m3;粘度0·021 7 Pa·s;固相颗粒平均直径2 mm;悬浮液体积分数10%。

    卧式螺旋卸料沉降离心机的处理液是在螺旋流道中流动的,考虑到转鼓与输送器之间转差很小,一般只有0·2% ~3·0%,对流道中流体流动影响甚小,可忽略不计,并且笔者只分析离心机的流场,所以只考虑离心机的沉降段。据此建立的离心机三维流道模型如图2所示。

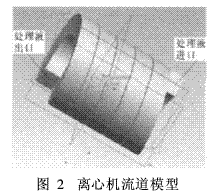
    2·5　网格划分

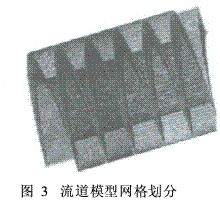
    采用C结构化网格(混合网格),划分网格后的模型如图3所示。

    2·6　边界条件

    进口边界取处理液的入口速度,取处理量为40m3/h,模型入口截面积为0·006 54m2,故进口速度为1·7m/s。同时,确定第2相的体积分数为10%。处理液出口设为压力出口,表压为0。流道的固体壁面定义为旋转壁面,旋转角速度为167·55 rad/s。对于紊流需要说明性质,假设流场为全湍流场,速度入口的流动充分发展,入口的湍流强度为5%,湍流粘性比为10%。当残差下降到10-5且进、出口的流量误差小于5%时,认为计算收敛。

    3·数值计算结果及分析

    笔者对离心机内流场的分析主要包括速度场、压力场、各相体积分数分布及流道内处理液的轨迹。计算结果见图4~图9。

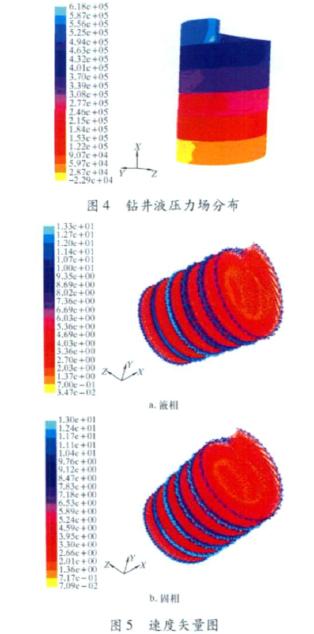
    由图4可以看出,在离心机的转鼓进口壁面压力最大,约为6·2×105Pa,在出口压力最小,大约为3×104Pa,最小的部位甚至为负压。由图5可以看出,钻井液进入离心机后,钻井液的速度场在转鼓壁面处速度最大,其中液相最大值约为13·3 m/s,固相最大速度约为13·0 m/s,而在中心处速度大约为0·7 m/s。由图5还可以看出,钻井液通过进口管进入离心机后产生了强烈的旋流,沿径向速度矢量逐渐增大。

    钻井液发生固液分离后,各相按一定的比例分布。液相的体积分数如图6a所示。

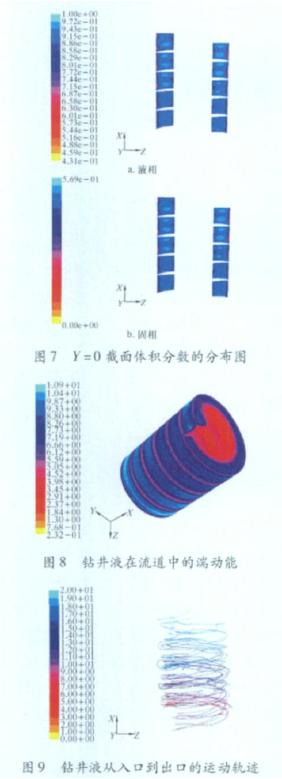
    由图6a和图7a可以看出,离心机从入口到出口处的液相体积分数逐渐增大,到出口处液相体积分数将近100%;由图7b和图9可以看出,固相颗粒体积分数的分布刚好与液相相反。这说明固相颗粒在这个过程中逐渐被脱除,有力地证明了钻井液在离心机内进行了较充分的固液分离。由图7还可以看出,在垂直于旋转轴的截面内,液相含量随着半径的增大而减小,固相含量随着半径的增大而增大。这是因为离心力与半径的平方成正比关系,在强旋流场中,高密度的固相沿径向向外运动抛向壁面,实现与液相的分离。

    由图8可以看出,转鼓内钻井液沿径向的湍动能逐渐增大,这是因为沿径向速度增大,撞击加强。由图9可以直观地看到钻井液从离心机入口到出口的运动轨迹。明显反映出液流轨迹为螺旋线,并且不光滑,有时出现小漩涡。这是因为钻井液在运动过程中存在湍动。

    4　结　论

    (1)对钻井液离心机内离心力场中钻井液流动速度进行了分析,并应用Fluent软件对钻井液离心机内流场进行了分析,结果与实际情况相符。

    (2)用这种方法对流场进行分析能解决目前对钻井液离心机内流场进行分析时,主要考虑稳定状态下的流动情况而不能反映复杂情况下真实流动情况的问题。如果再使之与相兼容的数据计算软件相结合,实现最佳分离效果显示,将对卧式螺旋卸料沉降离心机的设计有较大帮助。

    参　考　文　献

    [1]　赵国珍,张明洪,李君裕·钻井振动筛的工作原理与测试技术[M]·北京:石油工业出版社, 1996·

    [2]　孙启才,金鼎五·离心机原理结构与设计计算[M]·北京:机械工业出版社, 1987: 44·

    [3]　魏春琳,曾　实·离心机流场非稳态过程的初步数值模拟[J]·同位素, 2006 (1): 7-11·

    [4]　刘洪斌·钻井液离心机工作理论研究[D]·成都:西南石油大学, 2006: 48-51·

    [5]　王福军·计算流体动力学分析———CFD软件原理与应用[M]·北京:清华大学出版社, 2007: 116-124·

    第一作者简介:徐　倩,女,讲师,生于1974年,1997年毕业于西南石油学院机械系, 2002年获该校硕士学位,主要从事振动与动态测试、无损检测等方面的科研与教学工作。地址: (610500)四川省成都市。E-mai:l xx-qq0609@ 163·com。