离心机法校准加速度计不确定度的统计模拟算法

离心机法校准加速度计不确定度的统计模拟算法

乔仁晓1孟晓风2李皎1戴冬冰1

    (1.天狮学院自动化学院,天津301700;2.北京航空航天大学仪器光电学院,北京100191)

    摘要：加速度计精密离心机法校准的复杂性,使误差源的不确定度传播系数不满足显式解析、可导和近似线性的条件,因而无法应用常规的微积分方法求解。统计模拟方法是复杂测量不确定度计算的有效方法。通过模拟产生转速和半径随机矢量的多次实现值,经数据变换和最小二乘拟合得到加速度计方程系数的样本空间,最后用统计方法求得系数的不确定度,与离心机实验法校准结果比较,具有较高的一致性,证明了统计模拟方法的有效性。

    关键词：离心机；加速度计；校准；不确定度；统计；模拟

    中图分类号：TB9文献标识码:A国家标准学科分类代码：120.1470

    1·引言

    高精度惯导加速度计的静态特性校准主要通过精密离心机实现,离心机输出加速度的精度是决定加速度计静态方程系数估计精度的根本因素。离心机输出加速度量值大小由转速和工作半径确定,输出精度也主要取决于转速与工作半径的精度,并受失准角等因素影响[1]。随着航空航天、国防军工等尖端领域对线加速度计精度要求的不断提高,离心机的输出精度也必须进一步提高,从而要求工作半径和转速的测量、控制精度必须进一步提高。由于无法通过求导得到误差源不确定度传播系数的显式解析表达式,使得基于微积分的常规误差传递分析方法难以实现。近年来,蒙特卡罗统计方法被应用于复杂测量的不确定度估计,并得到国际计量局(BIPM)等国际组织的认可和推行[2-3]。本文通过模拟直接测量物理量的量值和数据变换,得到多维、非线性间接测量结果的样本,用统计的方法得到最终测量结果不确定度。

    2·不确定度统计模拟基本原理

    统计模拟方法又称为蒙特卡罗方法(MonteCarlo method),是一种以概率统计为基础的数值计算方法。它能比较逼真地描述和模拟事物的特征和物理过程。特别是对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题,如复杂的随机问题和非线性问题,蒙特卡罗方法是一种有效的求出数值解的方法。在测试计量领域,由于测量过程中往往存在许多随机因素,蒙特卡罗方法特别适合模拟测量过程中的各种误差因素的影响,近几年来被广泛应用于测量不确定度的评定[4-8]。不确定度统计模拟分析过程包括源数据仿真、数据变换、统计综合3部分。源数据仿真是指根据n个不确定度来源的概率分布信息模拟生成对应的n维随机变量的实现值;数据变换是根据测量的实际物理过程和数学处理算法对n维随机变量进行运算变换,得到间接测量结果。这两个过程重复多次,得到间接测量结果的一个样本空间;统计综合就是对间接测量结果样本空间的样本进行统计分析得到最终的数据结果[9]。具体过程如图1所示。

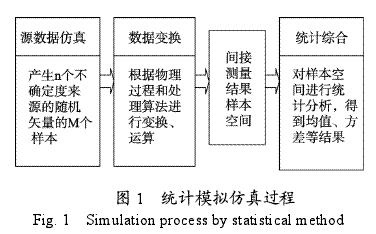
    3·加速度计系数不确定度统计模拟

    3.1加速度计离心机法校准建模

    线加速度计的三次多项式静态输入输出特性模型为：

    式中:a为沿离心机IA轴(输入轴)方向的输入加速度,e为加速度计输出值;ki,i=0,1,2,3为静态特性方程的各次项系数。

    作为标准装置的精密离心机,在忽略其他误差因素的情况下,输出加速度主要取决于离心机工作半径R和转速ω,关系式为：

    3)统计综合

    根据样本空间数据,拟合得到随机变量K的概率分布函数向量

    计算加速度计各次项系数估计值ki及其标准测量不确定度u(ki)。其中积分区间为整个样本空间Ω。

    4·统计模拟分析实例

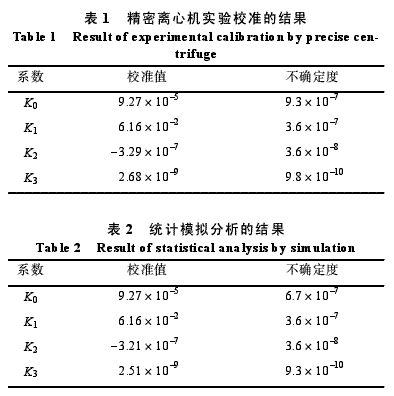
    分别用精密离心机实验法和统计模拟数值方法对某加速度计静态特性方程系数进行不确定度分析。表1为用精密离心机LXJ-40实验校准的结果,表2为用统计模拟方法10 000次仿真值统计分析的结果[10]。由表中数据可以看出,两种方法的校准结果具有较好的一致性。特别是作为主成分的一次项系数估计值及其不确定度估计值都有很高的准确度。偏值系数不确定度uk0值有较明显差别但量级相同,这是由于在统计模拟方法中只对主体变量ω和R的随机误差进行了仿真而忽略了一些次要误差因素,如加速度计输出值测量误差ue等因素的影响,而这些因素在实际离心机试验中都产生影响。

    另外,无论是统计仿真,还是实际离心机试验,加速度点数的选择和起始点的位置都会对最终结果产生微小的影响。

    5·结论

    传统的不确定度评定方法在某些复杂间接测量中遇到困难。现代计算机技术的飞速发展使计算机容量和运算速度大大提高,特别是虚拟化技术、网格计算、云计算技术的发展和应用,使得大样本容量的复杂运算的仿真变得容易实现[11-15],为近几年来逐渐发展的以大规模运算为基础的统计模拟方法提供了技术手段。在拥有足够概率分布信息的情况下,统计模拟方法既能同时对绝对误差和相对误差的影响进行合乎实际的仿真,并避开复杂的有时甚至难以实现的不确定度合成计算问题,得到稳定、可信的测量不确定度结果,又能对单个误差因素的影响进行仿真计算,便于精密测量仪器及实验方法的精度分析与设计。

参考文献:

[1]IEEE Std 836-2001.IEEE recommended practice forprecision

centrifuge testing of linear accelerometers[S].

[2]BIPM/JCGM.Draft for discussion:Guide to the expres-sion of

uncertainty in measurement supplement 1.Nu-merical Method for the

Propagation of Distribution[M].2001.

    [3]倪永勤.虚拟环境的间接测量不确定度评定与处理[J].微计算机信息,2007,23(4):103-105.

    [4]赵宇,陈松涛,钱键.Monte-Carlo法在测量不确定度评定中的应用[J].仪器仪表学报,2004,25(4):501-504.

    [5]王中宇.一种小样本虚拟仪器不确定度评定新方法[J].计量学报,2008,29(4):882-885.

    [6]陈晓怀,薄晓静,王宏涛.基于蒙特卡洛方法的测量不确定度的合成[J].仪器仪表学报,2005,26(8):760-761.

    [7]刘智敏.用MC仿真计算不确定度[J].中国计量学院学报[J].2005,16(1):2-4.

    [8]CHRISTOS E P,HIO Y.Uncertainty estimation andMonte Carlo simulation method[J].Flow Measure-ment and Instrumentation.2001:291-298.

    [9]崔孝海,曲璐.蒙特卡罗方法在微波功率测量不确定度分析中的应用[J].计量学报,2008,29(1):95-97.

    [10]乔仁晓.线加速度计精密离心机法校准建模与误差补偿[D].北京:北京航空航天大学,2009:80-95.

    [11]雷开彬,马志霞.分段线性网格模型编辑技术[J].西南民族大学学报,2008,34(3):577-583.

    [12]陈全,邓倩妮.云计算及其关键技术[J].计算机应用,2009,(9):2-6.

    [13]雷贤卿.圆度误差的网格搜索算法[J].仪器仪表学报,2008,29(11):2324-2329.

    [14]陈康,郑纬民.云计算:系统实例与研究现状[J].软件学报.2009,20(5):1337-1348.

    [15]许栋.微分网格处理技术[D].杭州:浙江大学,2006:3-25.