分形树状通道换热器内的流动换热特性
分形树状通道换热器内的流动换热特性
陈永平,杨迎春,施明恒,吴嘉峰
(东南大学能源与环境学院,江苏南京 210096)
摘 要:建立了分形树状通道换热器中层流流动与传热的三维稳态模型,采用流固耦合计算方法对入口水力直径为4 mm的矩形截面树状通道内流动换热进行了数值模拟,重点研究了分叉效应对传热的强化机理和换热器受热面的温度分布。研究结果表明:分叉处形成的二次流能有效地强化换热;与传统的蛇形通道相比,分形树状通道换热器具有温度均匀性好、压降小的明显优势。在相同入口雷诺数时,分形树状通道换热器受热面的最大温差远小于蛇形通道换热器,另外,分形树状通道的层流流动压降较之蛇形流道可减小50%以上。同时,加工了分形树状通道换热器及蛇形通道换热器各一套,对数值模拟结果进行了实验验证。实验值与模拟值能较好地吻合,证明了所建流动换热三维数值模型正确可信。
关键词:分形;换热器;流动;传热;均温性
中图分类号: V211·3; TK124 文献标识码:A
文章编号:1000-6893(2010)03-0472-08
可靠高效的热控系统是保障航空飞行器安全飞行的首要前提之一,随着航空飞行器制造技术的迅捷发展,其机载电子、电气设备的热可靠性指标也越来越苛刻,这就对机载换热器件的换热能力、泵功消耗以及温度均匀性提出了更高的要求。因此,在航空热控系统中,迫切需要研发结构优化的新型换热设备以实现高效冷却、散热。
仿生学经常能为设备优化提供有益启示。比如,人体的呼吸循环系统是一个非常高效的传热传质系统,人体中血管、气管和淋巴管都是从宏观尺度开始不断分叉到细胞尺度,在这些分叉中,高层次和低层次的分叉结构都是相似的,该种结构被B.B.Mandelbrot[1]称为分形结构。如将此分形结构应用于机载换热器件的设计研发,应能大大提高其热有效性,且由于通道呈树网状分布,可使换热表面的温度分布更加均衡。分形树状通道换热器即是受此思想启迪而发展起来的一种新型高效冷却、散热技术。
近年来,在分形结构流动换热研究领域已经取得了一定的进展,研究表明,分形结构对于提高系统的传热传质效率具有很强的促进作用[2-13]。A.Bejan等[2]借鉴分形理论,提出了一套用于电子器件冷却的树状结构换热系统设计方案,并且指出该结构的泵功消耗与流动阻力较之平行结构大为减小。D.V.Pence等[3-5]在圆形散热表面上设计了一套分形结构换热器,但是考虑到常规的电子芯片大多为矩形表面,故该类圆形散热器件的应用范围相对比较狭窄。可是,单层矩形树状结构却无法实现流体循环,针对这一问题,Y.P.Chen等[6]设计了一系列适用于矩形表面的三明治结构分形树状换热器,使得分形结构更具实用性,研究发现,分形结构换热器与传统的平行通道换热器相比具有更强的散热能力和热有效性。另外,为指导传热传质系统的优化设计,A.Bejan等[14]又在分形理论的基础上提出了一套用于系统优化设计的自构建理论。
S.M.Senn等[15]对Y.P.Chen等[6]提出的分形树状结构中的层流流动换热和压降进行了数值模拟。X.Q.Wang等[16-17]分别对适用于圆形和矩形表面电子芯片散热的分形树状换热器进行了流动换热研究,结果表明,分形通道壁面的温度均匀性明显优于平行通道。W.Wechsatol等[18]通过研究T型通道中的层流和湍流流动,提出在日趋微型化的电子芯片散热中,不可忽视分叉效应对于强化换热的关键作用。
但是,由于受到分形结构复杂性和计算负荷较大的限制,现有的数值研究大多为一维或二维模型,即使少量的三维工作也并未很好考虑流固耦合。分形树状通道换热器中传热传质机理尚未得到全面揭示,尤其是分叉对流动和换热的影响研究不够全面,能够更直观地体现其优越均温性的受热面温度分布研究也非常缺乏。为此,本文针对Y.P.Chen等[6]提出的三明治结构分形通道设计方案,建立了恒热流条件下层流流动换热的三维稳态模型,采用流固耦合计算方法对分形树状通道换热器内流动换热进行了数值模拟,重点研究了分形树状通道换热器分叉处二次流的强化换热作用及受热表面的温度分布特性,并与传统蛇形通道进行了比较。同时,还加工了分形树状和蛇形通道换热器各一套,对数值模拟结果进行了实验验证。
1 分形网络理论设计
如图1所示,参照人体呼吸系统的分形结构设计通道换热器,分形分叉网络生成方法如下:
①如图1(a)所示,每一段通道在下一层次都有两个分支,即N= 2,且Ф= 180°。
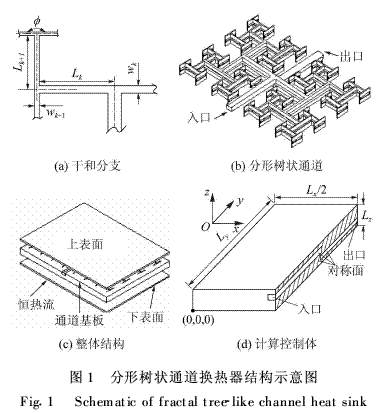
②k+1层次段的长度与k层次段长度的比值为

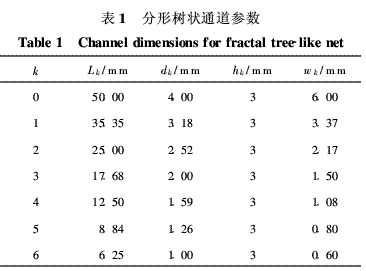
式中:d0为初始通道水力直径。现有研究表明[1],哺乳动物肺部支气管分叉树结构的指数Δ=3,鉴于肺中的空气流动和传热过程相当有效,故选择Δ=3作为水力直径分形维数。通道分布如图1(b)所示,通道级数为6,为了使冷却流体能自由循环且散热效果均匀,通道分为上、下两层。下层通道除了出口与上层通道的进口方向相反外,其他都相同。各级通道均为矩形截面且深度h一致。上层通道中的最高级分叉末端皆有通孔与下层通道的分叉末端相连通。分形树状通道换热器的整体结构见图1(c),由上、中、下3块铝板制成,中间层通道基板上下表面上布置分形通道。如图1(d)所示,换热器关于x=Lx/2平面对称,为了减少计算负荷,取整体的1/2为计算控制体。表1给出了分形树状通道的几何参数。
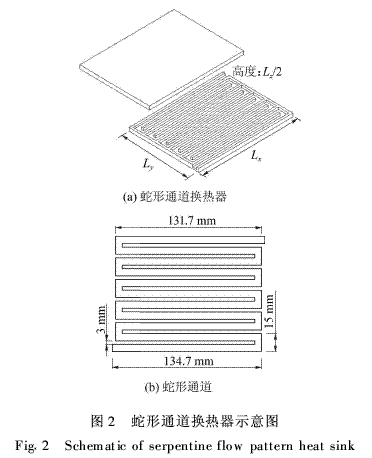
另外,设计与分形树状通道换热器具有相同受热面积、通道换热面积和入口几何参数的蛇形通道,以比较两者的温度均匀性和压降。蛇形通道如图2所示。在图1和图2中的换热器外型尺寸:Lx=138 mm,Ly=101·8 mm,Lz=16 mm。
2 数学模型
在计算控制体中(如图1(d)所示),上表面和3个侧面均为绝热边界条件,下表面为恒热流边界条件,其热流密度q=2·5 W/cm2。根据换热器的对称性,定义x=Lx/2平面为对称边界条件。用去离子水作为冷却介质,入口水温为20℃,给定流体入口速度。在层流、常物性以及忽略体积力作用等假设的基础上,建立三维稳态流动和传热耦合模型。
2·1 控制方程

2·2 边界条件
(1)流体的速度边界条件
在流固交界面上有流体无滑移边界条件


2·3 数值求解
根据分形树状结构的对称性,以x=Lx/2为对称面,取0≤x≤Lx/2,0≤y≤Ly,0≤z≤Lz的部分作为计算控制体。由于分形通道呈网状布置且各级通道尺寸存在较大差异,其结构较之传统直通道远为复杂;再者,考虑到流固耦合作用和分叉处附近出现的二次流,为保证计算精度,特对分形通道和固体部分均采用非结构网格,并在分叉处附近进行局部网格加密。另外,采用不同网格尺寸进行网格独立性检测,确保本文数值计算解均为网格独立的解。为减小扩散误差,采用二阶迎风格式离散控制方程。
基于控制容积有限差分法和求解压力耦合方程的半隐式(Semi-implicit Method for PressureLinked Equation,SIMPLE)算法求解控制方程式(5)~式(8)。当流体速度残差小于10-7,温度残差小于10-8,且进出口质量守恒和计算控制体能量守恒,即认为计算结果收敛。
3 结果分析与讨论
3·1 流动特性
分叉结构使得流体在通道中流经每一个分叉时均产生二次流,本文给出了一分叉处xOy截面和yOz截面的速度分布,截面位置如图3所示,其对应的速度如图4所示。
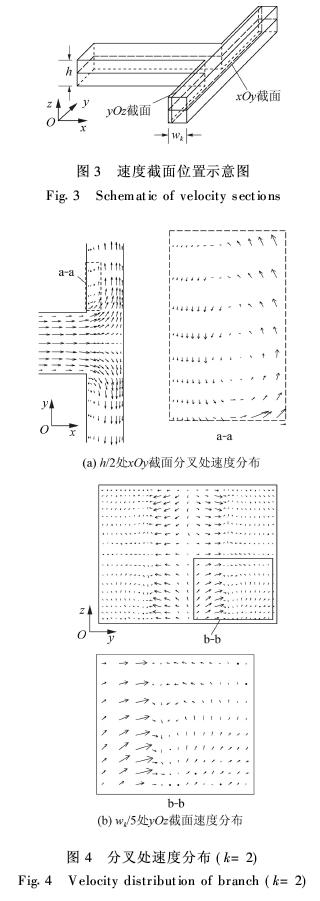
图4(a)为xOy截面分叉速度分布及分叉处二次流局部放大图,在通道分叉处流体由沿x方向流动碰到壁面转为沿y向流动,在内侧壁面分叉点附近形成了二次流,即流体在分叉点附近产生回流和分离现象。图4(b)分别为yOz截面速度分布及其1/4放大图,可以看出,中间层流体与近壁面流体之间形成漩涡。这种二次流促进了流道中近壁面高温流体与中间层低温流体的相互混合,并伴随流体射流冲刷壁面作用,从而强化了流动换热。
需要指出的是,尽管在分形通道分叉处形成的二次流在强化换热的同时也带来了一定的压降损耗,且随循环层次的增加,通道尺度的减小将导致单位流量流体的单位长度压降随之增加,但是,更应注意到分形通道具有流体流量的分散作用,它实质上类似一流动的优化分散器,该结构可使各单元流体分散流动,流动距离较之具有相同流固换热面积、集中流动的蛇形结构中流动距离大为减小,比如,本文中分形结构的流体流动距离(上下两层)为311·24 mm,而蛇形通道中流体的流动距离为1 202·5 mm,前者仅为后者的25·9%。流动长度的大比例缩短不仅有效地抵消了分叉及尺度缩小所导致的压损增加,且使得分形结构在总体上与蛇形通道相比具有压降小的明显优势。图5给出了两种通道换热器的压降Δp随入口雷诺数Rek=0的变化情况。在相同入口雷诺数时,流体层流流动压降仅为蛇形流道中的一半,与S.M.Senn等[16]的结论基本一致。
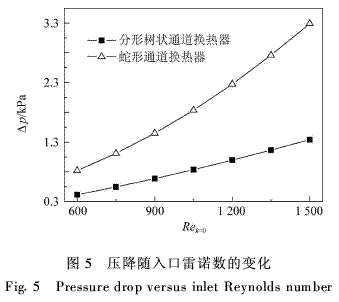
3·2 温度分布
图6给出了相同入口雷诺数时,分形树状通道和蛇形通道受热面的温度分布。两种通道的换热器具有相同入口几何参数、相同通道换热面积、相同受热面积以及相同外型尺寸。从图6可以看出两种通道换热器的受热面温度分布有较大的差别。在分形网络结构中,各级通道之间的换热是相互关联的,其中最为明显的是0级通道与其相邻的末级通道之间的相互影响,因此,最低温度出现在如图6(a)所示的换热器中心位置,并从该位置向外周温度逐渐升高,但总体温差不大。而蛇形换热器通道之间的换热影响较小,入口侧与出口侧温差较大。显然,前者在温度均匀性方面具有突出的优势。

在本文中,均温性以恒热流条件下受热面上出现的最高温度tb,max和最低温度tb,min之差加以表征。定义受热面的最大温差为Δtmax= tb,max-tb,min(18)
相同热流条件下,Δtmax越小,其均温性越强。图7给出了具有相同入口几何参数、相同通道换热面积、相同受热面积以及相同外型尺寸的分形树状通道换热器和蛇形通道换热器均温性的比较。由图可知,随着入口雷诺数的增加,两种换热器的最大温差均逐渐减小且变化趋势逐渐平缓,但是分形树状通道换热器的最大温差远小于蛇形通道换热器。再一次验证了分形树状换热通道具备优越的均温性。
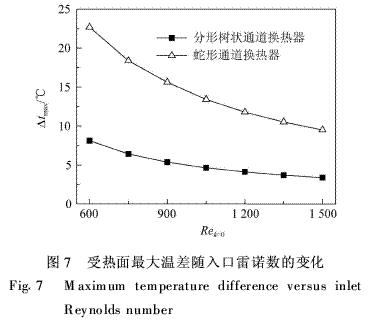
4 实验验证
4·1 实验装置
为验证所建层流流动换热三维模型的正确性,分别加工了一套与数值模拟所用结构尺寸相同的分形树状通道换热器和蛇形通道换热器,测量了两套换热器的受热面温度分布及进出口压力差。实验测试系统如图8所示。

分形树状通道换热器的上、下盖板和通道基板用螺栓和Ο型垫圈密封连接,电加热块和换热器之间用螺栓固定,接触面之间涂导热胶以减少接触热阻。整个实验段外包保温材料减少散热损失。蛇形通道换热器的安装也与之类似。实验中,采用电加热块提供恒热流,通过改变加热功率实现换热工况调节,输入功率由功率表测得。冷却介质为恒温水浴提供的20°C去离子水,通过调节阀门的开度以提供不同的冷却条件。采用玻璃转子流量计测量流量,用数字差压传感器测量进出口压力差。热电偶信号和差压传感器信号均由Agilent 34970A数据采集仪采集。
4·2实验结果
根据数值模拟中分形树状通道换热器和蛇形通道换热器受热面温度分布特点在受热面上布置具有代表性的测温点,并按照温度从低到高的顺序对测温点进行编号,如图9所示。
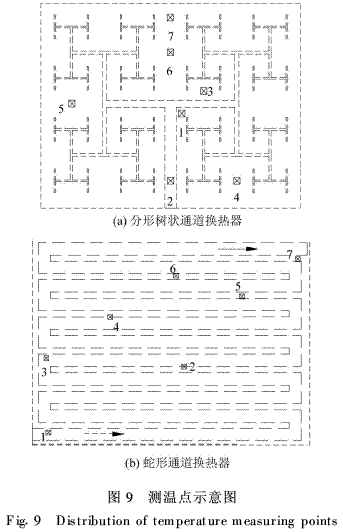
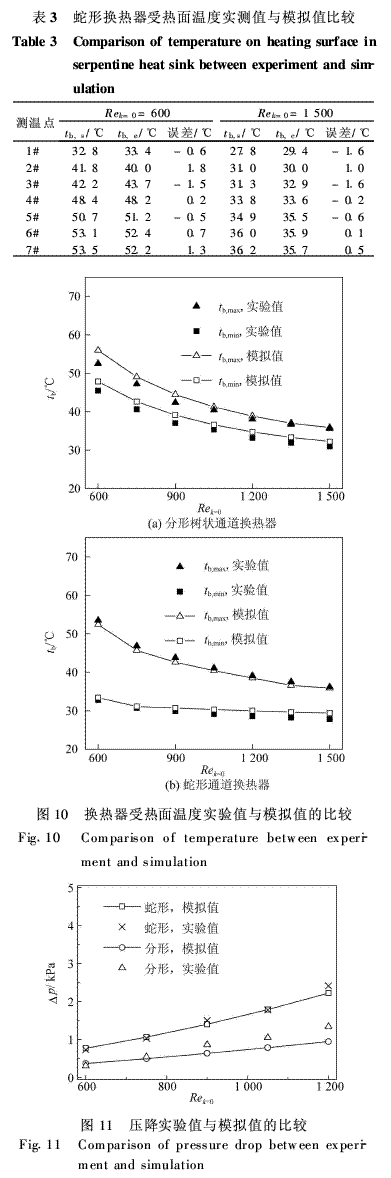
表2和表3分别列出了分形树状通道换热器和蛇形通道换热器在入口雷诺数分别为600和1 500时,7个测温点处的温度实测值和模拟值。可以看出,两表中实测数据皆从1#到7#依次升高,与模拟值的变化趋势一致。图10给出了两套换热器在不同入口雷诺数时受热面上实测最高、最低温度tb,e与模拟最高、最低温度tb,s的比较。从表2、表3和图10均可以看出,两套换热器温度实验数据与模拟值皆吻合较好。图11给出了不同入口雷诺数时,分形树状通道换热器和蛇形通道换热器沿程压降实验测量值与模拟值的比较,可以看出,压降的实验数据与模拟值同样基本吻合。这就证明本文所建立的流动换热三维模型准确可靠。
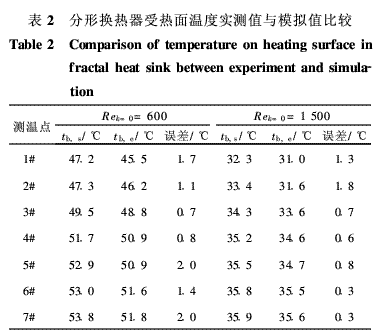
5 结 论
(1)在分形树状通道内,流体流经每一个分叉时在分叉点附近形成二次流,即产生回流和分离现象。这种二次流促进了流道中近壁层的高温流体与中心处的低温流体间的相互混合,并伴随流体射流冲刷壁面作用,从而强化了流动换热。
(2)与传统的蛇形通道相比,分形树状通道换热器具有温度均匀性好、压降小的明显优势,在航空热控系统中有着广阔的应用前景。在相同入口雷诺数时,分形树状通道换热器受热面的最大温差Δtmax远小于蛇形通道换热器,且随着入口雷诺数的增加,Δtmax逐渐减小。另外,分形树状通道的层流流动压降较之蛇形流道可减小50%以上。
(3)本文压降和温度的模拟值与实验测量值均能较好地吻合,这证明本文所建三维稳态模型准确可信。
参考文献:略
标签:
相关技术
2、如涉及作品内容、版权和其它问题,请在30日内与本网联系,我们将在第一时间作出适当处理!有关作品版权事宜请联系:+86-571-88970062
- 大港油田新型装置填补国内分层注水技术空白
- 齐二机床启动质量提升管理系列研讨会 共绘高质量发展蓝图
- 洛轴再次入选河南省创新龙头企业
- 中油测井改革举措为基层发展赋能
- 国家标准《压力管道规范 长输管道》正式发布
- 中通协2024年度重要产品技术鉴定工作回顾
- 永嘉3家企业入选2024年浙江省企业技术中心认定名单
- 百利二通中标中国华能集团有限公司2024-2026年电动执行装置及备件框架协议采购项目
- 辽河油田储气库群优化运行提升“冲峰”能力
- 整合多方资源优势 探索融合发展路径 西南油气田“天然气+”打造绿色增长极
- 第十七届上海国际化工装备博览会(CTEF2025)
- 沈鼓集团顺利通过国家智能制造能力成熟度三级评估