气体离心机二维供料射流流场数值模拟

气体离心机二维供料射流流场的数值模拟

姜东君 　王黎明 　曾实

(清华大学工程物理系  北京100084)

    摘要：为研究气体离心机供料射流的流动状况,采用数值求解二维Navier-Stokes方程组的方法对其进行了模拟,计算得到了不同供料角度下的流场分布。结果表明,供料射流对离心机流场在径向和轴向上的分布都有影响;供料角度为0°时,气体在轴向上反复膨胀、压缩,形成膨胀波和激波,对径向的影响较小;供料角度为45°和90°时,射流对轴向的影响减弱,对径向流动的影响显著增强。由计算结果可知,离心机环流的计算中应当对供料条件进行修正。

    关键词：供料射流;离心机;二维Navier-Stokes方程组;激波

    中图分类号:O35文献标识码:A文章编号:1000-0054(2008)08-1287-03

    为了提高气体离心机的分离性能,通常在其内部引入二次环流[1]。供取料驱动是较为常用的驱动方式,由于取料口位于离心机侧壁附近,因此关于取料对二次环流影响的研究比较深入,对取料器附近流场的研究也比较多[2-4],而对位于中心区域的供料射流的研究相对较少。由于供料射流影响离心机内部流场的粘性边界,因而对环流的影响也必须加以考虑。在以前的研究中,供料驱动条件往往是根据供料量和一定的假设在粘性边界上给出的,如采用均匀亚声速流动条件[5],或者采用满足一定函数分布的源项[6]。以上各种假设不能够反映真实的流动状况,因此,有必要对气体离心机供料射流进行研究。

    离心机内的供料射流同工程中遇到的射流问题有较大不同,工程中射流的周围为均匀流场,在没有供料射流时,离心机内的流场满足旋转刚体假设[1],即压强和密度在径向上呈指数分布,速度为线性分布,当工作气体射入离心机后,将受到强旋流场的影响,一方面受径向压强梯度的影响,在径向上的膨胀波被压缩;另一方面受到旋转的影响而具有角向动量。

    本文通过数值求解二维轴对称Navier-Stokes方程组,模拟离心机内的二维轴对称供料射流流场,并对不同供料角度下的流场进行了分析,为实际离心机供料射流流场的研究打下了基础。

    1　计算模型

    在本文的计算中,离心机参数按照Iguacu模型[5]给定,其转子半径为6cm,长径比为8,侧壁线速度为600m/s,即旋转角速度为104rad/s,侧壁压强为13.3kPa。采用二维轴对称供料模型,如图1所示。本文计算了3种供料模型,其区别在于射流角度的不同,如图1a、1b和1c所示,射流角度α分别为0°、45°和90°。

    2　计算方法

    2.1　控制方程控制方程为二维轴对称Navier-Stokes方程组:

    由于在射流出口为超声速,流动为紊流状态,在计算中选用Realizablek-ε湍流模型。

    2.2　计算方法

    在计算中采用有限体积法对控制方程进行离散,计算中使用二阶迎风格式,隐式迭代。

    3　边界条件和初始条

    件离心机处于高速旋转状态,因此在计算中采用旋转坐标系,旋转角速度为1×104rad/s。

    计算中用到的边界如图1所示,具体设置如下。

    供料入口:给定来流的压强、速度和温度。

    转子侧壁:旋转壁面,给定壁面的旋转速度(600m/s)和温度(300K)。

    压力出口:按照刚体旋转条件[1]设定背压:

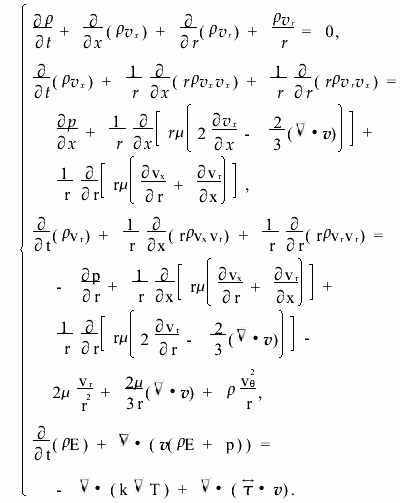
    底部端盖:旋转的壁面条件,给定壁面的旋转速度和温度。

    在计算中,以无供料时的离心机流场(即旋转刚体假设)作为初场,压强分布见式(1),密度为

    4　计算结果及分析

    计算中使用的气体为UF6,其相对分子量为352。入口条件给定为500Pa,温度为300K,速度为0。在此供料条件下,计算得到了射流角度分别为0°、45°和90°3种供料模型的流场。

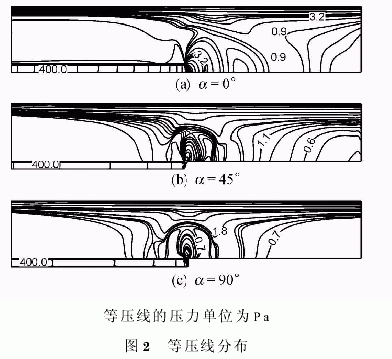
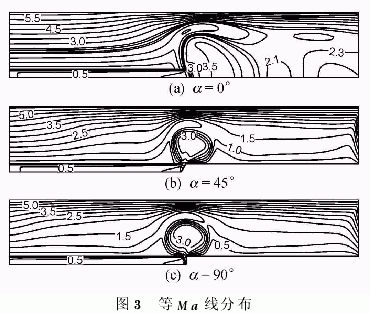
    图2给出了3种供料模型下的等压线分布,相应的等马赫数线分布如图3所示。在供料角度为0°情况下,当气体进入离心机后,迅速膨胀,在径向上受到离心机压力梯度的影响,被迅速压缩;在轴向上存在压缩-膨胀-再压缩-再膨胀的过程。当供料角度为45°时,气体在径向上的膨胀压缩过程较为明显,轴向上的分布已经明显减弱。在供料角度为90°的情况下,气体在进入离心机内之前,在管口处形成了激波,经过激波后,气体的速度明显降低,可以看到,形成的膨胀-压缩波基本上是以出口为中心的圆弧,在轴向上呈对称分布,与供料角度为45°的情况相比,对离心机侧壁处的影响减弱。在图3中可以观察到同样的流动现象。

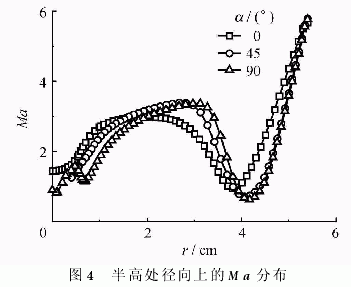
    对于不同的供料模型,图4分别给出了在半高处(x=0.24m)径向上的Ma分布。从图中可以看到,在r=0.04～0.06m之间,在0°供料角条件下,Ma基本保持线性分布;供料角为45°和90°两种情况下,Ma的分布基本相同,也呈线性分布,但其分布曲线位于供料角为0°的曲线下方。这表明当供料角度增大后,径向速度增大,从而对离心机流场施加了更大的影响。

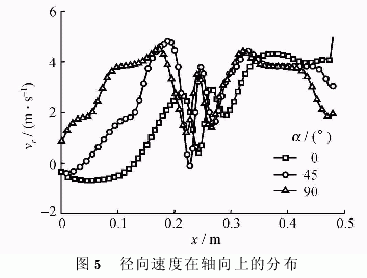
    供料射流对离心机流场的最主要影响是对近侧壁处环流的干扰,因此环流计算内边界处,轴向和径向速度在轴向上的分布是本文所关心的。图5和图6给出了半径r=0.048m处轴向上的径向和轴向速度分布曲线,从中可以观察到,对于文中计算的3种供料条件,径向速度在轴向上的分布比较复杂,在3种供料角度下,都存在不均匀分布。但一般离心机环流计算经常是将供料假设为一股均匀的亚声速流动,这是应当修正的。在供料角为45°和90°时,轴向速度则基本上以半高处为中心对称分布。

    5　结论和讨论

    本文通过求解二维轴对称Navier-Stokes方程组模拟了二维离心机射流流场,采用有限体积法离散,使用二阶隐式迎风格式迭代计算,得到了不同供料角度下的流场分布。对计算结果的分析表明:

    1)射流对离心机流场在径向上和轴向上的分布都有影响;

    2)在供料角度为0°时,气体在轴向上反复膨胀、压缩,对径向上的流场影响较小;

    3)在供料角为45°和90°时,射流对轴向的影响减弱,对径向流动的影响显著增强;

    4)无论在何种供料条件下,供料射流所造成的流动参数(包括径向速度和轴向速度)在轴向上的变化,在离心机环流计算中都应当被考虑。

    本文计算的是二维情况下供料射流对离心机流场的影响,实际的供料模型更为复杂,需要进行三维数值模拟。