卧螺离心机流场的三维数值模拟

卧螺离心机流场的三维数值模拟

郑胜飞1, 2,任　欣1, 2,谢林君1, 2　

 (1.浙江工业大学过程装备与控制工程研究所,浙江杭州　310032;　　2.浙江工业大学机械制造及自动化教育部重点实验室,浙江杭州　310032)　　

    摘要：针对卧螺离心机理论研究的不足之处,采用Fluent软件中的RSM模型和DPM模型模拟卧螺离心机三维流场,通过适当的求解策略,得到流场内的压力分布和速度分布。结果表明,整个液环角速度滞后约为0. 83,模拟液压约为理论值的65%,颗粒沉降时间与理论计算结果符合较好,为进一步深入研究奠定了基础。

    关键词：化工机械;卧螺离心机;数值模拟;角速度滞后;颗粒沉降

    中图分类号：TQ051. 8　　　文献标志码：A　　　文章编号：1005-2895(2009)06-0026-04

    0　引言

    卧螺离心机是一种广泛应用于石油、化工、冶金、医药、食品、轻工等行业的机械,既可以用于液相澄清,也可以用于固相脱水。由于离心分离过程的复杂性和多样性,例如悬浮液的物理性能和浓度非常容易变化,特别是固相颗粒的大小形状和运动的杂乱状态带来的问题,给理论和试验研究造成了极大的难题。计算流体力学的发展,为卧螺离心机流场研究开辟了新的方向[1]1。在此基础上,采用Fluent软件对卧螺离心机流场进行数值模拟,研究了其流动规律和液-固分离特点。

    1　模型简化及网格创建

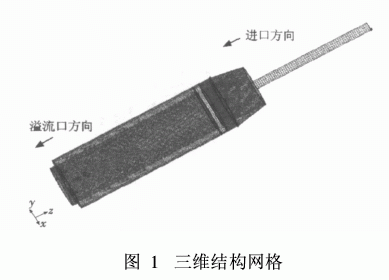
    卧螺离心机中转鼓和螺旋以一定的差转速运行,实现悬浮液的分离及沉渣的排出。目前Fluent尚无直接对应的模型可进行模拟,因此本文对流域作了适当的简化:未考虑螺旋的作用。主要计算尺寸如下:转鼓长度L=800 mm,外直径D=200 mm,液层深度h=2mm。采用定常方式计算流场, Fluent中高精度数值差分格式,例如二阶迎风差格式,QUICK格式,主要针对于结构网格,应用于非结构网格效果并不理想。因此对于旋转流动,要以少量计算时间取得较精确的数值模拟结果,须采用结构网格进行求解。将卧螺离心机的几何结构划分为多个子块,针对每个子块采用Cooper方法创建结构化网格,共得到66 434个网格、221 895个面、85 114个节点。在实体交界面处,重合边界设置为Interface面。网格如图1所示。

    2　边界条件及求解策略

    2.1　边界条件

    入口设定为速度入口边界,通过指定入口处的湍流强度和水力直径来设定边界条件,入口湍流强度按经验公式[2]计算。卧螺离心机出口为溢流出口,出口处的压力等于大气压,设定出口为压力出口边界条件。转鼓壁设定为无滑移条件,转鼓转速设置为ω=39rad/s,对于自由液面处壁面,设置为有滑移。

    2.2　求解策略

    卧螺离心机内部流场属于旋转流动,流动较复杂,为获取较精确解,计算过程中采用了以下求解步骤:1)压力差值采用PRESTO!格式; 2)采用边界网格自适应加密壁面附近网格; 3)改变压力、速度的亚松驰参数,减少为0. 1; 4)使用步进解,首先计算没有旋转影响的流动,也就是说先在边界条件中设定壁面为静止壁面,至收敛后,再设置壁面速度,只求解动量方程至收敛,关闭湍流方程和雷诺应力方程,最后打开所有的方程获取完全的耦合解; 5)在开始计算时,采用较低的旋转速度,然后逐渐增加直至所需要的操作条件。

    3　模拟结果分析[3-11]

    3.1　压力分布

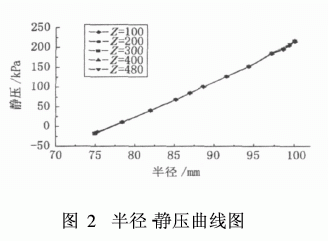
    图2是根据Z=100,Z=200,Z=300,Z=400,Z=580这5个截面沿半径方向的静压力值绘制而成的。从图上可以看出静压力沿着半径方向从0增加到225 kPa,入口处及溢流口都与大气相连,因此,在此二处的静压力接近零值。不同截面上的半径-压力关系基本趋于重合,说明静压力轴向梯度几乎为零;对于径向压力分布,图显示压力与半径成抛物线关系,与卧螺离心机相对照的是,模拟所得静压即为离心机中存在的离心液压。根据模拟结果可知,离心液压为理论计算值的65. 6%左右,这对于离心机转鼓强度优化设计具有一定的指导作用。

    3.2　速度分布

    图3分别为转鼓圆柱段3个不同阶段的轴向速度折线图,比较3个折线图,可以把转鼓内轴向流速分布规律划分为3个阶段。其中Z取粗略值可把400~600 mm归为第1阶段,由图(a)可知,在流体刚进入转鼓后,经过短暂的调整适应,流速分布呈现出一定的规律性,半径在75~84 mm范围内,流动沿Z轴负方向(即溢流口方向),在同一径向液层深度上,随着Z值变小,速度的绝对值不断减小;在84~100 mm范围内,流速沿Z轴正向,在同一Z处,沿半径方向,速度先增大后减小至鼓壁处为零。由此可知,流速在此阶段存在一个较大的回流。由于离心机平均轴向流速必定指向溢流口,因此图形分布也显示速度负方向的积分面积大于正方向。经过此阶段后流动转入第2阶段(Z=200~400 mm),此阶段速度分布均匀,从图上看折线呈水平状态。同时该阶段也是较符合层流理论的阶段。之后,流动接近溢流口,且存在转鼓壁几何结构的限制,流动发生了较大的变化,不再是层流流动状态。Z在0~200 mm范围属于第3阶段,该阶段内流速方向与第1阶段恰好相反,半径在75~85 mm范围内,流速为正, 85~100 mm范围内,流速为负。

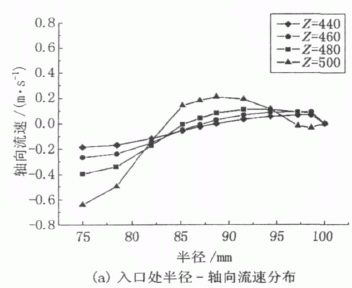
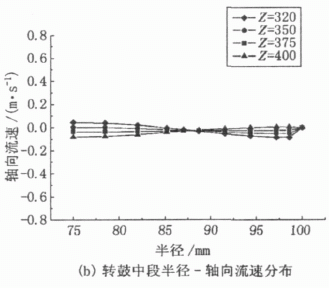
图 3　不同阶段轴速分布曲线

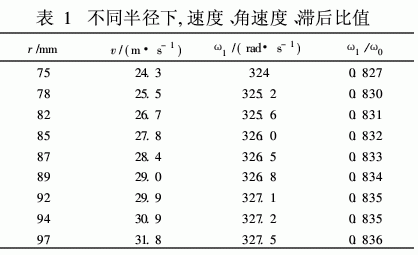
    表1是根据模拟所得到切向速度,周向滞后比例与半径的关系。本文中液层深度为25 mm,于是r/r2=0·75。根据文献[1]47数据,可得出自由液面处ω/ω0的取值范围为(0. 78~0. 91)。由于文献中该作者并未指明自由液面层处a值是在直径为多大的卧螺离心机中测定,也未指出转鼓的转速以及测量时的液层深度,因此只能进行定性的验证。模拟中根据200mm卧螺离心机的处理量范围,设定流量Q=4×10-4m3/s,远小于文献中的试验流量,照常理推a值应当大于0. 91,可模拟求得a值为0.827。事实上文献中角速度滞后曲线得出的理论前提为层流理论,即假定速度分量ur,uφ,uZ仅与半径有关,而与φ,Z和时间t无关,且ur为0。而本文所进行的模拟则考虑了3者与φ和Z的关系,且认为运动为复杂的湍流流动,由此存在着一定的差距也不足为奇。同时,由于计算机运算能力的限制,以及偏微分方程的在离散过程中产生截断误差,也是造成误差的原因之一。

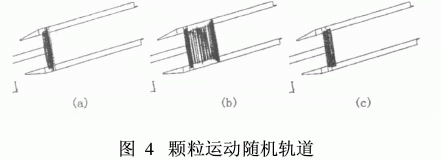
    3.3　颗粒相运动分析

    采用DPM模型加入颗粒相后,分析颗粒的运动轨迹。图4为10μm颗粒在湍流作用下不同的运动轨迹。图4(a)表明颗粒在离心力作用下很快就从自由液面运动到了转鼓壁,图4(b)显示颗粒沿轴向运动较长时间后方沉降至转鼓壁,图4(c)中颗粒在足够时间步长内陷入死循环而无法被分离。考虑到螺旋存在的影响,小直径颗粒沉降所需时间较长,在碰到转鼓壁之前,将先与螺旋叶片接触,在轴向速度较小情况下,颗粒与螺旋发生碰撞反弹,从而对颗粒沉降产生不利影响。这种情况下,增大螺距,能同时提高沉渣输送能力和提高分离效率,但螺旋升角太大,容易使渣周向打滑、堵塞、排渣困难。因此应当综合考虑2者需求,以取合理值。

    3.4　离心力场中颗粒沉降速度

    液固2相的密度不同,使颗粒相对于液体存在1个径向速度,从而实现2相的分离。在计算颗粒沉降速度时,首先要根据Ret判断流型,而Ret中含有待求的ut,所以计算需要采用试差法。下表分别计算不同直径颗粒在ω=324 rad/s,自由液面处颗粒的的沉降速度。

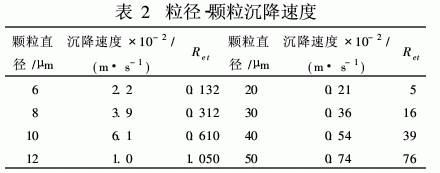
    为了验证Fluent计算颗粒运动的正确性,在表1的基础上,计算出颗粒位于半径R=100 mm处的理论沉降速度。将液环半径除以最大和最小沉降速度,即可得到颗粒所需最小和最大沉降时间,并与模拟得到的沉降时间进行比较,见图5。

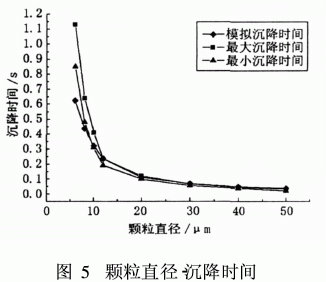
    观察图5中3条曲线走向,可知颗粒直径与沉降时间存在着二次曲线关系。直径大于12μm以上的颗粒,模拟值与实际值吻合较好,可见Fluent关于颗粒计算符合斯托克斯公式。而6, 8, 10这3种颗粒存在不同程度的偏差。颗粒直径越小,则偏差范围愈大究其原因,可以发现在6μm时颗粒的沉降速度为2.×10-2m/s,当颗粒直径下降至1μm时,沉降速度小至6. 1×10-4m/s。由于Fluent采用有限体积法求解方程,因此在偏微分方程组转化为代数方程组后,不可避免地存在着截断误差。一方面,可以通过提高细化网格减少截断误差;另一方面由于计算机容量的限制提高网格将使得计算量成倍增加。随着颗粒直径的减小,当前计算条件下,将无法得到精确解。

    4　结语

    采用RSM模型和DPM模型对卧螺离心机两相流场进行三维数值模拟,进一步明确了流场内各物理量的分布及液固分离机理。有如下结论:

    1)在当前模拟结构条件下,所得离心液压值约为理论计算值的65. 6%,这对于优化转鼓结构能起到一定的指导作用。

    2)沿转鼓长度方向,轴向流速分布并不均匀,除在中间段与层流理论下的轴向速度分布较接近外,入口及溢流口处的流速分布皆变化较大。

    3)转鼓长度对对于大直径颗粒分离影响不大,这时影响分离的主要原因是湍流及螺旋的搅动。

    4)用Fluent软件计算颗粒轨道,尤其对于小直径颗粒的运动轨迹,还需要进一步提高网格精度和计算机运算能力,以获得更精确计算结果。

参考文献:

[1]　孙启才,金鼎五.离心机原理结构与设计计算[M].北京:机械工业出版社, 1987.

[2]　王福军.计算流体动力学分析: CFD软件原理与应用[M].北京:清华大学出版社, 2004.

[3]　周强,程乐鸣,骆仲泱.方形卧式分离器两相流场的数值模拟[J].动力工程, 2004, 24(4): 567-571.

[4]　耿丽萍,杨茉,曹玮.高炉淤泥旋流法颗粒分离的数值模拟[J].工程热物理学报, 2004, 25(4): 628-630.

[5]　赵斌娟,袁寿其,刘厚林.基于Mixture多相流模型计算双流道泵全流道内固液两相湍流[J].农业工程学报, 2008, 24(1): 7-12.

[6]　王春林,马庆勇,李婷婷.搅拌浆液池固-液两相流搅拌的数值模拟[J].排灌机械, 2007, 25(6): 38-41.

[7]　林玮,王乃宁.旋风分离器内三维两相流场的数值模拟[J].动力工程, 1999, 19(1): 72-76.

[8]　赖艳萍,赖维,卢晓江.圆柱型水力旋流器流场CFD软件的数值模拟[J].轻工机械, 2007, 25(3): 20-22.

[9]　曹亚裙,陈建,王灿星,等.油烟机用多叶离心通风机内部流动的数值模拟[J].机电工程, 2009, 26(6): 38-40.

[10]　王卫国,周慎杰.圆柱旋流器多相流场的数值分析[J].化工装备技术, 2006, 27(2): 17-19.

[11]　黄志新,钱才富,范德顺.沉降离心机圆形转鼓内液面速率的数值模拟[J].北京化工大学学报, 2007, 34(6): 645-648.[信息·简讯]